協和音・不協和音が分かる純正律の話
コード理論を学んでみようとした時「この音は協和音で、これは不協和音になります。」といった説明があって、それを感覚だけに頼るよりも何故そうなるのかを納得出来れば楽なのではないでしょうか。そもそも音が協和するとはどういう事なのかという話をします。

平均律と純正律
音律(音階)にも幾つかの種類が有ります。
そしてそれらは皆、ある部分を重視して上手くいく様になっていれば、別の何処かに問題点がある。といった具合で、全てが問題なく纏まった理想的な音律というのは存在しないそうです。
昔、14世紀頃まで吟遊詩人たちが奏でていたのはピタゴラス音律という音律でした。
これは単音でメロディーを弾くには美しいのですが、3音以上の音を同時に出して和音を弾くには向いていなかったそうです。
それを修正して作られたのが純正律です。純正律は協和した和音が弾ける事を主目的とした音律です。
その後、更に中全律など何種類かの音律が考案されました。
そして、19世紀中頃に、当時完成されつつあったピアノと伴に現在一般的に使用される音律である平均律が広まっていきます。
ピアノと平均律の普及、それは機能性と一般化の革命でした。
それは、調律されたピアノさえあれば、誰でも正しく鍵盤をたたけば、どの調の音階でもすぐに弾くことが出来て、曲の途中で転調も自由にできる。というアドバンテージです。
鍵盤に慣れていて他の楽器に馴染みが薄いと、この事は当たり前のように感じるかも知れませんが、「素人はまず正しい音階の音を出すのが困難」という楽器は結構ありますし、純正律だと例えばCメジャー(ハ長調)に調律するとDmのコード(レ・ファ・ラの和音)は使えず、その為にDマイナー(ニ短調)の曲を弾くには調律し直さないといけません。もちろん、この二つの調での転調も出来ません。
これらの問題が解決できる事に加え、1オクターブを均等な12の半音に分けるという明快さも平均律のメリットです。
しかし、冒頭にも書いた様に理想的な音律というのは存在せず、平均律にもやはり問題点が有ります。
平均律が機能性と引換に失くしたもの、それは「純正な和音の響き」です。
厳密で純正な和音というのは純正律のもので、平均律の和音は純正律の近似なのです。
一応お断りしておきますが、別に正しい和音は純正律だからこれからは純正律を使おうとか言いたい訳では有りません。たとえ厳密には少しずれた近似であっても平均律の和音は充分に機能しますし、平均律の分かりやすさと機能性は他に代えがたいものだと思います。
ただ、和音とか音の協和とかの根拠を周波数に求めて説明すると、どうしても「この和音は純正律でいうと周波数比が…。」みたいな話になるんですね。
ですから、正しい和音とは何なのか、それを導き出す純正律の音階とはどんな構成になっているのかを少し見てみたいと思います。
純正律の音階
まずはご存知の方も多いでしょうが、前提となる知識の確認から。
・音階内の音の音程差の呼び方
音階は、まず基準となる基音(主音)を定めてそれを第1音とし、以降、第2音~第7音までが並び、第8音が基音のオクターブ上になります。
音階の音程差は「何度」という風に呼びます。
一度はユニゾンとも言い、同じ音程を指します。ですから隣の音との音程差が二度になります。
基音から数えると第二音との音程差が二度、第三音との音程差が三度です。
・音程と周波数
音程というのは物理的に言えば音の周波数です。そして周波数と音程の関係は等比が等差になる対数的変化になっています。
例えば、周波数が2倍になれば、音程は1オクターブ上がります。更に2倍で4倍なら、2オクターブ、8倍なら3オクターブ、という風に1:2という周波数の比率が1オクターブという音程差に当たる訳です。
ですから、2音間の音程差はその2音の周波数比で表せます
純正律の音階では各音間の周波数比が全て整数比になります。
そしてその整数比は「自然倍音」が基になっています。
・自然倍音
シンセの音作りの回でも同じ様な説明を書きましたが、通常の楽器の音は単純に音程として聞こえる一つの周波数だけではなく、その上の周波数が足し合わされて成り立っています。この上に重なっている周波数を倍音と言います。
自然倍音とは整数倍音とも言い、2倍、3倍、4倍、…といった整数倍の倍音です。
非整数倍音というのも有りますが、これは金属を叩いたり、引っ掻いたりした時の音等の、その音独特の響きとして感じられます。音程感が無いので音楽的には、雑音とまで言わなくてもあまり重視されず、倍音といえば自然倍音を指す事が多いです。
純正律の音階は2倍、3倍、4倍、5倍の自然倍音から導き出されます。
・純正律の音階を計算してみる
では例として自然倍音から純正律の長調の音階の周波数比を計算してみましょう。
周波数が2倍で1オクターブ上になる事は先に書いた通りです。では、3倍、5倍、が何の音になるかという所から始めます。
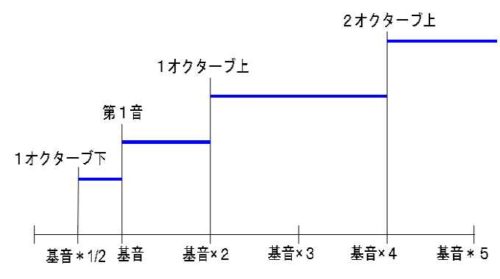
まず3倍音。3倍ということは基音1のオクターブ上(2倍)より高く、2オクターブ上(4倍)よりも低いので3倍音は1オクターブ上の音階になります。ですから1オクターブ下げてオクターブ内に持ってきます。1/2にすると1オクターブ下になりますので3倍音の1オクターブ下は基音の3/2倍という事になります。
この周波数3/2倍の音が純正律の第5音に当たります。音程差でいえば基音の五度上は基音の3/2倍という事です。
逆に基音の五度下も考えてみます。
五度上が3/2倍なので、基音は五度下の音の3/2倍という事ですから
基音:五度下の音= 3/2 : 1 = 1 : 2/3
ですので五度下の音は基音の2/3倍、1オクターブ上げて同じオクターブ内に持ってくると、4/3倍となります。
この基音の4/3倍の音は第4音に当たります。
次に5倍音。5倍音は2オクターブ上の音階になりますので1/4にしてオクターブ内に持ってくると5/4になります。これが第3音になります。
後はこれらを組み合わせて、第5音の三度上が第7音、第4音の三度上が第6音、第5音の五度上を1オクターブ下げて第2音とします。
第7音= 3/2 × 5/4 = 15/8
第6音= 4/3 × 5/4 = 5/3
第2音= 3/2 × 3/2 × 1/2 =9/8
となり、まとめると下のようになります。
| 第1音 | 第2音 | 第3音 | 第4音 | 第5音 | 第6音 | 第7音 | |
| 周波数比 | 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 |
協和性を量る一つの目安として、この周波数比が小さな数でシンプルな比率である程、協和性が高くなります。
基音との組み合わせで考えると最もシンプルな比率はオクターブですが、それに続いて第5音の3/2、第4音の4/3です。
3音の組み合わせをみると、基音から一つ飛ばしで、基音・第3音・第5音を組み合わせると
1 : 5/4 : 3/2 =4 : 5 : 6
のシンプルな比率となります。この比率は、第4音・第6音・基音の1オクターブ上と第5音・第7音・第2音の1オクターブ上の組み合わせでも同じになリます。
また、第3音・第5音・第7音と第6音・基音の1オクターブ上・第3音の1オクターブ上では
5/4 : 3/2 : 15/8 = 10 : 12 : 15
5/3 : 2 : 5/2 = 10 : 12 : 15
と、これも比較的シンプルな比率になります。
先に少し書きましたが第2音から同様に第2音・第4音・第6音と3音取ると
9/8 : 4/3 : 5/3 = 27 : 32 : 40
と、数字が大きくなり協和性が低い事が分かります。
理想的にはここも 10 : 12: 15 となって欲しい所なのですが、部分的に和音が崩れてしまうのが純正律の欠点の一つでも有ります。
比率が 4 :5 : 6 になる三和音を見ると基音と第3音、第3音と第5音は両方とも三度の関係ですが比率は 4 : 5 と 5 : 6 で違います。この二つの三度を区別して 4 : 5 を長三度、 5 : 6 を短三度といいます。
長調の音階には無い音ですが第2音と第3音の間に基音の短三度上(♭3)も 6/5 とシンプルな整数比の音になります。
同じく長調の音階外でシンプルな整数比になる音は第6音の下に♭6として 8/5 になる音が有ります。この音は第4音の短三度上にあたり、基音との音程差を♭6が短六度、長調の第6音を長六度と呼びます。
協和音とは
周波数比が小さな数のシンプルな比率の方が協和性が高い。と書きましたが、これも定義としては少し曖昧です。
協和音を厳密に定義しようとすると色々な要素があり、考え方によって様々な捉え方が出来ます。ですから協和性を推し量る基準は幾つか有っても、簡単で明確に「何がどうであれば協和音」と断言できる基準はないそうです。
また協和性は同じ和音でも違うオクターブで弾くと少し違いが有って、低い音域では協和音とは言い難いケースもあるそうです。
音楽理論で協和音と定められた音
とは言っても、実用的にはある程度定まってくるので、理論上協和音とされる音程差は決められています。
協和音とされるのは、「完全協和音」として、オクターブ、五度、四度。「不完全協和音」として長六度、短六度、長三度、短三度です。
二度と七度は不協和音とされます。
もちろんこれは不協和音は使えないとか、協和音の方が価値があるとか言う意味では有りません、使い方の問題ですね。
うなり/差音
ギターのチューニングをした事があるとか、やっているのを見た事があるという方ならご存知だと思うのですが、少しだけ周波数の違う音を同時に鳴らすと、周期的に音量が大きくなったり小さくなったりする「うなり」が発生します。
波形図にすると下の図のような感じです。
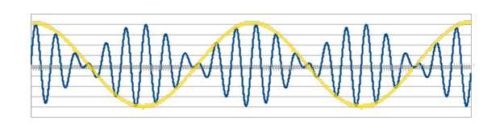
うなりの揺れは二つの音の周波数の差が大きい程、速い振動になります。周波数差が一定以上になると音として聞こえる速さの振動数になります。こうなると、もはや「うなり」ではなく、それ自体が音として聞こえるので、これを「差音」と呼びます。
周波数が適度に離れた二つの音を同時に鳴らすと差音が混ざって聞こえる訳ですから差音も協和性を左右する大きな要素となります。
差音の周波数は以下の様に求められます。
モデルとしてサイン波を考えると周波数の違う二つ音の足し合わせは
sin(2πat) + sin(2πbt) …a,b:周波数
となります。これに三角関数の和積の公式を当てはめると
sin(2πat) + sin(2πbt) = 2sin[2πt(a+b)/2]cos[2πt(a-b)/2]
となります。
数式だとピンと来ないと思いますが、要するに (a+b)/2 つまり元の二つ周波数の平均を周波数とするサイン波に 2cos[2πt(a-b)/2]を掛けたものです。
2を掛けるとアンプで増幅したように振幅が大きくなり2倍になります。
更にそこへ cos[2πt(a-b)/2]を掛けると、シンセでいうアンプモジュレーションになります。
上の図で言うと黄色い線が 2cos[2πt(a-b)/2]で、このcos[2πt(a-b)/2]が差音になるのですが、数式上だと大きくなってまた小さくなる塊の二つ分で1周期ですが、聴覚上は一塊は同じに聞こえますので、一つが1周期に感じられますから差音は
cos[2πt(a-b)]
となります。つまり元の二つの周波数の差が差音の周波数ですね。
音を重ねてみる
周波数比が少ない数でシンプルな比率は協和音になりますが、何故そうなるのかを考えると難しいので足し合わせた波形図で見てみることにします。
表計算ソフトでサイン波の足し合わせをグラフにしました。
順に見ていきたいと思います。
まず最も協和性が高いと思われる基音とその1オクターブ上の組み合わせから、
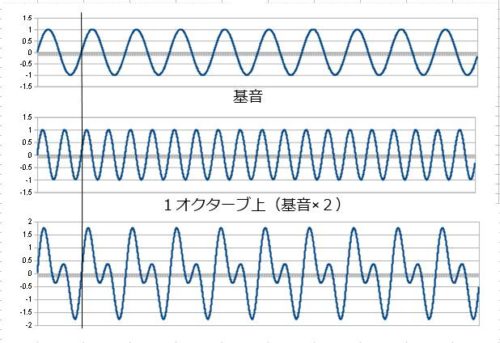
一番下が足し合わせた波形になります。
線の位置までが1周期になって、短い周期で規則正しく並んでいる様子が見て取れます。
こういう短い周期で規則性の高い波形となる組み合わせが協和性の高いと言って良いと思います。
次に完全協和音の基音と五度上、基音と四度上を見てみます。
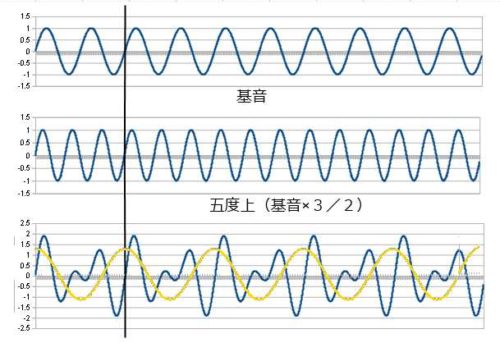
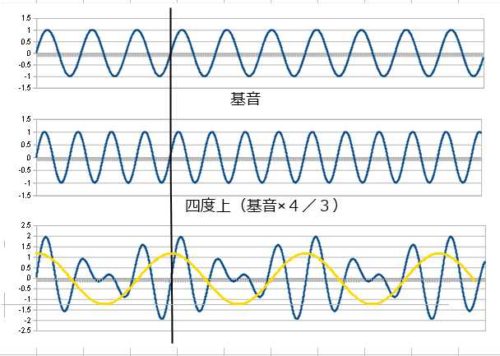
オクターブよりは周期が長くなりますが、まだ規則性の分かりやすい形ですね。
黄色線は差音を示していて、五度上の場合、差音の周波数は基音の 1/2 つまり基音の1オクターブ下になります。
四度上は差音の周波数は基音の 1/3 、これは2オクターブ下の第4音に当たります。
比べてみると四度上の方が周期も長く、やや複雑な波形になり、また差音も離れた音になるので、五度上に比べてやや協和性は低いと言えそうです。
次は不完全協和音の長三度と短三度です。
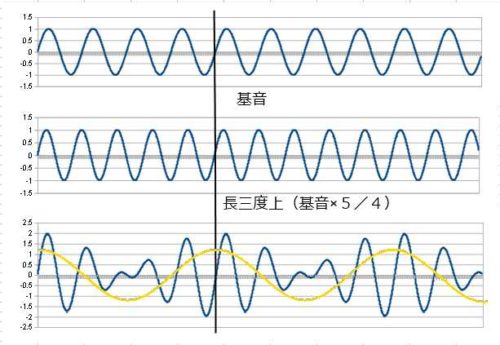
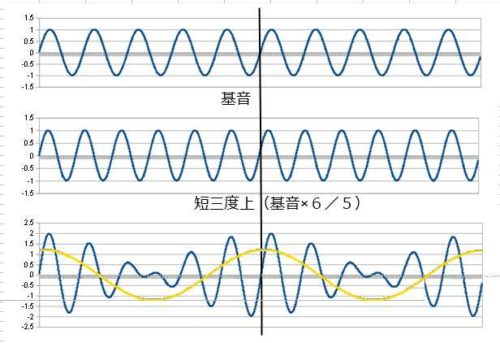
三度になると差音が見た目で分かりやすいですね。長三度は差音の周波数が基音の 1/4つまり2オクターブ下、短三度は基音の 1/5 、これは3オクターブ下の♭6に当たります。短三度は差音で違う音が混ざる事になりますね。
続いて長六度上と短六度上です。
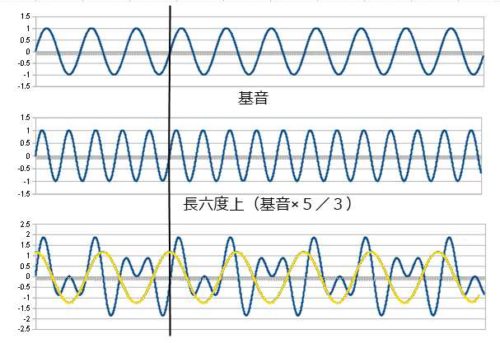
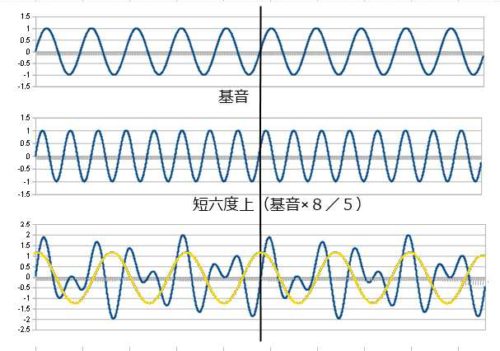
長六度は周期も短くまだ規則的な感じがします。短六度になると周期も少し長くなり、やや複雑な印象を受けますね。
差音は長六度が 2/3 、1オクターブ下の第4音ですね。短六度が 3/5 、1オクターブ下の♭3になります。
次から不協和音になります。二度から見てみます。
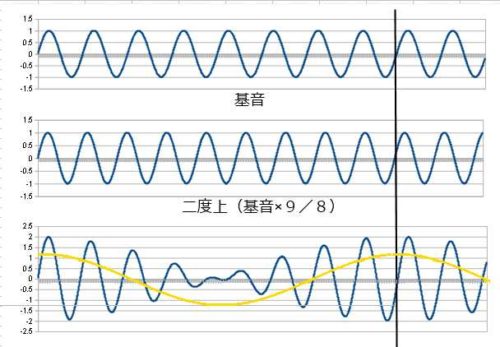
三度の周期が長くなった感じです。差音が基音の 1/8 、3オクターブ下の基音です。差音が低くなるので低音域で使うと音と聞こえるギリギリになりそうで、おそらくそれが音を聴いたら少し濁った感じになるのだと思います。周期は長くなりますが波形が複雑になった印象は受けないですね。不協和音ではありますが、テンションとして割りと使いやすいと思います。
続いて七度上です。
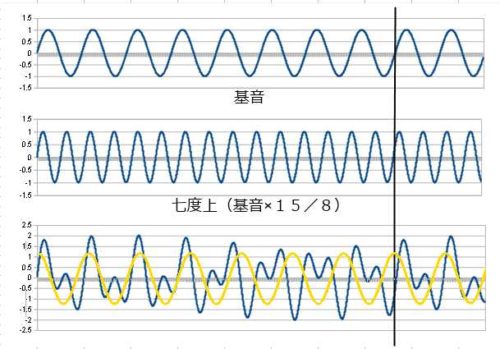
周期も長くなり、波の形もそれなりに複雑になりますが何と言うかちょっとおもしろい形ですね。パターンが変化していってますが不規則というより明らかにうねりのようなものが見えます。
この辺まで来ると割りと不安定感があります。この不安定感は同時に鳴らさなくてもあって、例えば長調のドレミを順に弾いていってドレミファソラシで止めると中途半端で「いっそドまでいけや」っていう感じがすると思います。これが自然短調(ナチュラルマイナー、鍵盤のラから初めて白鍵のみで構成されるのがAナチュラルマイナー)だとそうでもありません。この、上の主音に戻って落ち着こうとする性質から 15/8 の第7音は主音に導くという意味で導音と呼ばれます。ちなみにこういう不安定な音から安定感のある音にいって安心感を与える手法を「解決」といいます。
差音については音を聴いても私の耳では確信が持てないのですがそのままの周波数差の差音だと黄色い線の 7/8 になりますがこれが聞こえるのかどうか良く分かりません。
最後に不協和音らしい例を挙げたいと思います。
トライトーンと呼ばれる音程差で長調の音階で言うと第4音と第7音の関係がそれに当たります。平均律だと第4音→第7音も第7音→1オクターブ上の第4音もどちらも半音6個分で同じですが純正律だと
第4音:第7音= 32 : 45
第7音:1オクターブ上の第4音= 45 : 64
と少し違ってくるので純正律のトライトーンは2種類ある事になります。
下の図は 45 : 64 です。
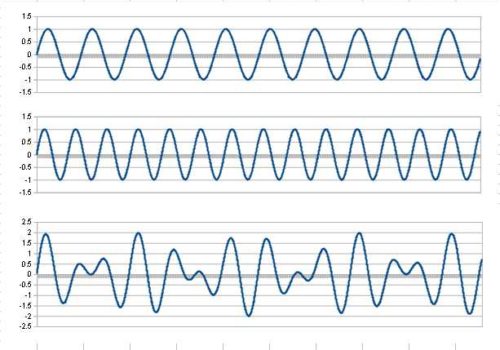
五度のパターンが崩れた様な感じですね。周期が長すぎて入りきっていない為、不規則で波形のパターンが読み取れませんが、こんな感じで基音の波45個分の長さで続きます。
差音も 19/45 と2オクターブ下の第6音と第7音の間の良く分からない音になります。
こうして見ても如何にも不協和音な感じですが、実際に聞いてみるとほんとに不安定で、ずっと聞いていると不安な気持ちになるところから昔は「音楽の悪魔」とか呼ばれていたそうです。
差音についてもう少し詳しく(蛇足)
今回の記事の目的は、二つの音を同時に鳴らした時の感覚は、音の周波数の比率と差音という物理的な側面とリンクしていてある程度解析可能であることを示し、実例で説明して音の協和/不協和の感覚を整理する参考にしていただく事です。
その目的に沿うなら前項までで終わっても良いです。以下の分は私自身が考えた事で、きちんと裏付けを取れていないので間違っている可能性もありますし、意味のある内容かどうかも分からないので面倒なら飛ばしてもらって構いません。
上に挙げた図を通して見て、音程差の離れた、計算に使った基音よりも1オクターブ上の方が近い六度上や七度上になると差音の周期をみてもピンと来ない気がしませんでしたか?
実際、差音の数式を導き出しているサイトでも「二つの音の周波数があまり大きく離れていない時」という前提を置いていたりします。
では、音程差が離れるとどうなるのか、という推察です。
その前に差音についてもう少し詳しく見てみます。
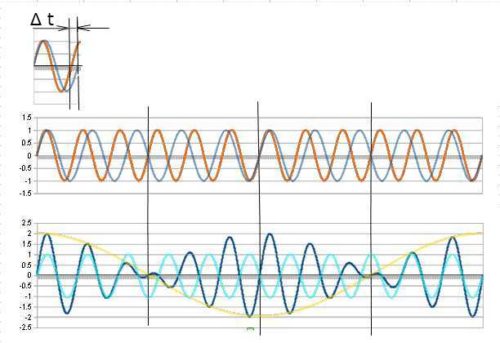
短三度の足し合わせた図です。線の色を変えて重ねています。
二つの波は、1周期毎に周期の時間差:Δtの分だけズレていきます。足し合わせるとそれぞれの頂点が近づいた時点では大きくなり、離れると小さくなりますのでうなり/差音が起こります。
下の足し合わせた波に重ねて表示してある水色の線は二つの周波数の平均を周波数としたサイン波です。水色の波が黄色の線に沿って振幅が変化しています。
次に七度上の足し合わせを同様の図にしてみます。

七度だと周波数が基音に対して 15/8 ですから周期の時間差:Δtが大きくなり、一周期で大きくズレてしまう為、対応するそれぞれの頂点が一周期毎に大きく位置関係を変えます。差音となる周波数差のコサイン波も周期が短くなりアウトラインに当てはまってはいますが内部の波形パターンが変わっていくので見た感じでこれで差音として聞こえるかどうか疑問に思ってしまいます。
周期の長さで言えば基音の波1個と七度の波2個の方が近いので七度の2周期分をセットで考えて、基音の波に対して七度の波2個セットが少しずつずれていくと考えてみます。七度の波2個ですから上側の頂点2個と下側の頂点2個あります。この4個のそれぞれの頂点が足し合わされた時の点を繋ぐ線を上側の分だけ書き込んだのが図の緑の線です。
計算式の細かな説明は省きますが、Δtは基音の周期時間の 1/15 になります。七度の波2周期の時間は基音の周期時間の 16/15 ですので、これでΔtを割って時間あたりのズレを計算すると時間tにつき (1/16)t 分ズレていく事になります。
緑の線は七度の波の頂点とその時の基音の値を足した値で、基音のサイン波はtに対して (1/16)t ずつズレますので緑の線は
1+sin[(1/16)t]
の初期位置を合わせたものになります。
波形図のうねりの様なパターンが気になって計算してみたのですが実際に周波数の設定を合わせたサイン波を聴いてみてもこの 1/16 のうねりが聴覚上どう影響しているのか私には分かりませんでした、もしかすると意味のない計算だったかも知れません。
最後に
今回の記事はコード理論に入る前に、そもそも協和音とは何なのかを説明しておきたかったので書きました。音楽理論に馴染みの無かった方は色々な言葉が急に出てきて戸惑ったかも知れませんが、今回、純正律で説明した二音の音程差の協和/不協和というのは、平均律でも基本的に同じですので、いきなりは覚えられないかも知れませんが、ある程度掴めたら作曲しようとした時に理論等に頼るだけでなく自分自身の実感として捉えやすいので楽しいかと思います。
今回の記事が多少なりともその助けになれば幸いです。
